Summary

The objective of this assignment is to practice:

1. reading and understanding legacy code, i.e. modules created by others,
2. using legacy code for your own needs,
3. creating useful data types and data structures,
4. documenting your work in form of a literate Haskell program.

The assignment is to be completed in teams of two.

In this assignment you will apply your functional programming skills to the domain of music. Your task is to write a program which takes information from a musical score and automatically generates very rudimentary accompaniment to the melody. You will base your solution on 1) a model of music expressed in the form of a Haskell library for musical structures called Haskore, and 2) a basic theory of musical harmony, expressed below a a set of simple rules to follow.

It may be worth noting that prior knowledge of music is not necessarily an advantage. Although the theory presented is hopefully correct, it is expressed in a way which most musicians are not familiar with and probably would not approve of. However, keep in mind that this is NOT an exercise in mastering music theory; it is an exercise in understanding a clear set of rules to follow and implementing the expected behaviour.

Please have a look at an exemplary solution of this assignment, by Linus Åkesson.

If you find the below presentation of the music theory basics as incomprehensible, you may try an alternative presented on the site Music Theory for Normal People, where the first section (and maybe the second as well) deals with fundamentals useful in this assignment.

Musical scores

Printed music, or scores, uses quite an elaborate notational system to communicate information to musicians so that they can play the song. Many songs are built on a melody with accompaniment and the score often gives the melody explicitly whereas the accompaniment is described as a more abstract harmonic structrure which the musician must translate to musical sounds. For example, in the score below, "Twinkle Twinkle Little Star", the notes show the melody and the harmonic structure of the accompaniment is presented as a sequence of chord symbols above the melody line. Click the score to hear the song.

Haskore music

Haskore is a library of Haskell modules which allows musical structures to be expressed in a declarative manner. This section gives a beginner's introduction to music and summarizes the most relevant parts of the Haskore tutorial.

From a technical point of view, music is simply a collection of notes. Each single note is primarily determined by its pitch (frequency) and its duration. When the note is played the resulting sound is further characterised by things like:

• which instrument it is played on
• how loud it is played
• how it is articulated, e.g. soft, aggressive, distinct, etc.

What makes music a bit more complex to approach than this are the conventions and the terminology which has developed over time, mainly regarding pitch and duration. Pitch is measured in equidistant discrete steps (called semitones) on a logarithmic frequency scale. This means that the frequency doubles over equal intervals. This interval is called an octave and consists of twelve semitones. On a piano this corresponds to the fact that an octave consists of seven white keys and five black keys.

Notes are by convention named by their position within the octave. The notes corresponding to the white piano keys are named with single letters C, D, E, F, G, A, and B. The notes corresponding to the black keys are named by their relationship to the neighboring white key as being a sharp (raised) or flat (lowered) version of it. for example, the note between F and G can be referred to as both F# (F sharp) and Gb (G flat).

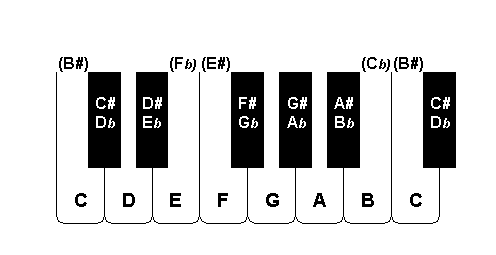
In Haskore these names within an octave are called a pitch classes. The pitch of a note is thus uniquely defined by the combination of a name (pitch class) and an octave. The following Haskell definitions therefore gives an appropriate model of musical pitch:

type Pitch = (PitchClass, Octave)
data PitchClass = Cf | C | Cs | Df | D | Ds | Ef |
                   E | Es | Ff | F | Fs | Gf | G |
                  Gs | Af | A | As | Bf | B | Bs
    deriving (Eq,Ord,Ix,Show)
type Octave = Int

The duration of individual notes are given by its nominal value which is measured in fractions of a bar. The duration of a half-note is thus 1/2 and the duration of an eighth-note is 1/8. In musical notation the nominal duration is indicated by the appearance of the note:

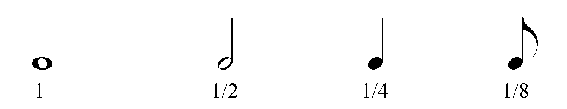
The actual duration corresponding to these nominal durations is then determined by a tempo declaration valid for the whole musical piece, or at least a larger part of it. A typical example of such a declaration is that tempo should be 120 quarter-notes per minute. The Haskore definition of the duration type is:

type Dur = Ratio Int

Musical qualities of the individual notes arise from how they are structured and organized in time. The Haskore library defines music with the following recursive algebraic data type (slightly simplified):

data Music = Note Pitch Dur [NoteAttribute] -- a note
           | Rest Dur           -- a rest (pause)
           | Music :+: Music    -- sequential composition
           | Music :=: Music    -- parallel composition
           | Tempo (Ratio Int) Music  -- scale the tempo
           | Trans Int Music    -- transpose (raise
                                -- or lower) all notes
           | Instr IName Music  -- select instrument
     deriving (Show, Eq)

A fairly loud C quarter-note in the fourth octave, for example, is a music object which can be expressed:

c4 = Note (C, 4) (1%4) [Volume 80]

The only note attribute we will be concerned with in this assignment is the volume. Its value ranges from 0 to 100.

The same note repeated three times and played by a flute can be expressed as:

Instr "flute" (c4 :+: c4 :+: c4)

As instrument you can either use names from the full list of instrument names in the General Midi standard which can be found in the Haskore manual, or names from the shorter list below:

"piano"
"vibes"
"bass"
"flute"
"sax"
"guitarr"
"violin"
"violins"
"drums"

To build various musical structures you can of course use the full expressive power of Haskell. A chord (a number of notes played simultaneousely can for example be expressed with a list comprehension:

cMajor = foldr1 (:=:) [ Note (x, 4) (1%2) [Volume 60] | x<-[C, E, G] ]

When you have built a music object in Haskore you normally want to listen to it. To do so you use the function test :: Music -> IO (). It generates a midi-file called test.mid which can be played with ordinary midi-players such as Windows Media Player or Winamp.

Harmonic theory (a.k.a. the rules)

Keys, scales and chords

A vital piece of information in a score is the key of the song (although how it is present in the score is not obvious to a non-musician). For example, the key of Twinkle, twinkle above is C major. A musical key has two components: a root, which is C in this case, and a harmonic quality which is either major or minor.

One of the things the key does is that it defines a scale which gives the (main) note supply for the song. A scale is a subset of the twelve notes in a full octave(the most commonly used scales consist of seven notes although scales with other numbers of notes do exist). A scale is usually described by stating the root of the scale, together with a scale pattern, which is a list of semitone distances from the root. For example the key scale of C major is shown below. The root is C and the semitone distance from the root for each of the notes are shown within parentheses.

This scale pattern is called the Ionian pattern, and it is used to generate the scales of all major keys. Similarily, the minor key scales are generated by the Aeolian pattern. These and a few other patterns are defined in the table below.

Ionian:		0, 2, 4, 5, 7, 9, 11		(Major)
Lydian:		0, 2, 4, 6, 7, 9, 11
Mixolydian:		0, 2, 4, 5, 7, 9, 10
Aeolian:		0, 2, 3, 5, 7, 8, 10		(Minor)
Dorian:		0, 2, 3, 5, 7, 9, 10
Phrygian:		0, 1, 3, 5, 7, 8, 10

The sequence of chord symbols which describe the harmonic structure of the accompaniment is called a chord progression. The chord progression, for example C F C G C etc. for Twinkle, twinkle, gives the main harmonic structure of the accompaniment. Often there is a single chord symbol for a whole bar, but sometimes the bar is split by two (or more) different symbols. A chord is simply a set of notes played simultaneously, for example {C,4; E,4; G,4} and each chord symbol designates a chord class, which is a set of chords which in a harmonic sense are equivalent. Formally, a chord class is similar to the concept of a key, in that it consists of a root and a harmonic quality. Unlike a key, however, a chord class has the additional information of a chord pattern, which is a subset of the scale (i.e., a further restriction of the note supply) with notes to build the chord from. For example the chord class F has F as its root, major as its harmonic quality and the basic triad as its chord pattern. The basic triad consist of the first, third and fifth notes in the scale of the chord (see chord scale below) and is the fundamental and most commonly used chord pattern. It  is for example the pattern of all the chords for Twinkle, twinkle. When the chord symbol consists of the root only, the "default" harmonic quality and chord pattern are major and basic triad respectively. An F minor chord has for example the symbol Fm.

The chord class also identifies a scale which gives a supply of notes available for accompaniment during this part of the song. This supply is called the chord scale and, as described above, the scale is defined by a root and a scale pattern. The root of the chord scale is simply the root of the chord class. The scale pattern, however, is a bit trickier to obtain. According to the theory of tonal music, this scale pattern depends on the so called function of the chord class. A full definition of this function is beyond the scope of this assignment, but an operational defintion sufficient for our purposes is that the function of a chord is given by the position of the root of the chord class with respect to the scale of the key together with the harmonic quality of the chord. For each such combination of harmonic quality and position in the key scale, the theory of tonal music associates a specific scale pattern. The table below shows some of these associations, that is, scale patterns for the most common major and minor chords in major keys. The scale patterns for more unusual chords have been omitted.

Position		Major chord		Minor chord
1		Ionian
2		Mixolydian		Dorian
3				Phrygian
4		Lydian
5		Mixolydian
6				Aeolian
7

 

Consider as an example a chord symbol G in Twinkle, twinkle. This symbol designates the chord class G major, that is the root is G and the harmonic quality is major. The key of the song is C major and in figure above showing the C major scale we see that G has position number five. In the table above we see that position five and a major chord identifies the mixolydian scale pattern. Finally, we apply this pattern to the root of the chord and obtain the chord scale as G(0), A(2), B(4), C(5), D(7), E(9), F(10). The numbers in parentheses here are the scale pattern applied.

The chords in the chord progression, and their associated scales, provide the necessary information for accompanying the melody. A rudimental accompaniment can be created with two parts: a bass line and a chord voicing. A bass line is basically a melody giving a fundamental rhythm and tone quality to the song. The bass line is typically played in the lower register, say, C,3-G,4 in Haskore notation. The chord voicing enhances the tonal quality of the song, thus creating a richer and fatter sound and is typically played in the mid register, say, E,4-G,5.

Generating bass lines

Bass lines in  popular music of today are often based on various stereotypes used in different musical genres. As a rough example of stereotypes, three different bass styles are shown below: Basic, Calypso, and Boogie. The notes indicate the rhythmic pattern of the bass lines. The number below each note shows what note in the chord scale to be used, starting with 1 as the root. The rhythmic pattern should be interpreted as sound or silence. Each bar is virtually divided into a number of beats, all having equal duration. The basic style consists of two beats (half notes), all beats sounding. The calypso style has a feeling of eight beats; the first two are silent (a quarter note rest), the following two are sounding (eighth notes), then another two beats of silence followed by two sounding beats. The boogie style, finally, consists of eight sounding beats (eighth notes).

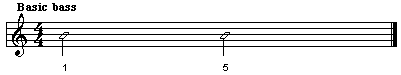
As an example, suppose we want to create boogie bass to a bar of Twinkle, twinkle. There is no bar with a G major chord class only, but to be able to build on our functional analysis of G major above, let us assume there was one. Keeping the notes in the interval C,3-G,4 ,the bass of this bar would then consist of a sequence of eight eighth-notes with the pitches {G,3 - D,4 - E,4 - D,4 - G,3 - D,4 - E,4 - D,4}.

Now we may turn to slightly more complex situation, which is very common in Twinkle, twinkle, namely that there is more than one chord symbol per bar. For example the third bar has first a G major chord class and then a C major. In the case of such split bars the bass is constructed by taking only the first half of the bass pattern and concatenating the notes generated by each of the chords.. A boogie bass for the third bar would thus consist of eighth-notes with pitches {G,3 - D,4 - E,4 - D,4 - C,3 - G,3 - A,3 - G,3} (The derivation of the C major chord scale is left as an exercise to the reader.) A basic bass for the same bar would be two half-notes with pitches {G,3 and C,3}

Generating chord voicing

The fundamental chord voicing is built on triads (a triad is three notes sounding simultaneously), changing in accordance with the chord symbols and the melody flow. The chord changes will thus represent three new melodic lines, although these are not really independent melodies but created for backing up the melody harmonically. The tones in a triad do not have to be chosen from a specific octave - from a harmonic point of view pitches with the same pitch class value but different octaves are equivalent (in fact, that is why pitches are represented as they are in Haskore). For example, a C major chord can consist of the triad {C,4;E,4;G,4} as well as {C,5;E,5;G,5}. Furthermore, the order of the tones in a triad needs not to be fixed. The first note is called the root and the others third and fifth, respectively. When the bottom note is changed to the third or the fifth instead of the root, different inversions are created (e.g., {E,4;G,4;C,5} and {G,4;C,5;E,5}). This freedom in terms of octaves and inversions means that there are many different chords to choose from for a specific chord class. And some choices will sound better than others. So the question is how to make good choices. Although this is essentially a part of the artistic skill of good musicians, some rules of thumb for good chord voicing does exist:

• A first rule of thumb is to keep all chord notes within a limited range. In this exercise E,4-G,5 is suitable.
• A second rule of thumb is to make the changes in the chord "melodies" as small as possible. Using only triads, there will be three such melodies: one consists of the sequence of bottom notes in all chords, a second of the sequence of middle notes and the third of the sequence of all top notes. The change in a melody is measured in semitones. For example going from the C major chord {E,4;G,4;C,5}to the G major chord {D,4;G,4;B,4} changes the bottom melody 2 semitones, the middle melody 0 semitones, and the top melody 1 semitone. The total change is the sum of the changes in the melodies, in this case 3. Theoretically you can optimize these changes over the whole song but in this assignment it will be sufficient to do it one chord at a time.
• And as a third rule of thumb you usually get a "tighter" sound by keeping the tones in the triad as close to each other as possible (closed voicing). For example,  {E,4;G,4;C,5} is a C major chord that has a closed voicing while {E,4;C,5;G,5}is a C major chord that has not.  

Preparation

The preparation for the assignment consists of studying at least chapters 1, 3 and 10 of the Haskore tutorial and trying out the examples. The Haskore2010.zip file available in /usr/local/cs/EDAN40/ (on student machines) or here: Haskore2010.zip, contains a slightly modified and rudimentarily tested variant of Haskore fitting ghc 7.4.1 (i.e. it should fit the assignment needs).
In order to verify it copy it to a directory you own, unzip, invoke ghci and say
:l ChildSong6.lhs
and then
test childSong6
This should create a file called test.mid that should be playable by your favourite midi player, e.g. timidity.

It has been pointed out to me that Haskore2010 above does not work with ghc 7.6.3. The offending module is HaskoreUtils.hs, that uses catch which no longer can be found. To remedy this, insert the following line somewhere by the beginning of the module:
import Control.Exception hiding (assert) (and make sure that your ghc finds the Control.Exception module:-)

Any information about issues related to running this variant of Haskore using ghc 7.8.x will be much appreciated.

Assignment

1. Melodies

Melodies often consist of repeating parts, sometimes transposed or otherwise modified each time. Transcribe the melody of  Twinkle Twinkle Little Star into Haskore in a way that such structures are made explicit. You may want to look at Appendix C in the Haskore tutorial where another song is encoded in this way. Use the utilities in the module TestHaskore to output the results as a midi file which can be played on the computers which have sound cards.

2. Accompaniments

The result of the main part of the assignment is Haskell module for automatic generation of accompaniment to a given melody. The module should be written as a literate Haskell program (.lhs-file) which, at the same time as it is an executable and correct program, is an essay which explains the types, data structures and functions you have chosen to create the musical accompaniment described above. This explanation must be self-contained in the sense that it is understandable without access to the Haskore tutorial (so please think about how you present your solution). An example of a literate program is the Haskore tutorial itself.

a) Write a function, autoBass which automatically generates a bass line. Given a bass pattern, a chord progression, and the key of the song, autoBass returns the bass line as a Haskore music object.

autoBass :: BassStyle -> Key -> ChordProgression -> Music

Test the function with basic, calypso, and boogie styles on the chord progression for Twinkle Twinkle Little Star.

b) Write a function, autoChord, which automatically generates a chord voicing including the guidelines for good voicing described above. Given a key and a chord progression, autoChord returns the chord voicing as a Haskore music object.

autoChord :: Key -> ChordProgression -> Music

Again, test the function on Twinkle, twinkle.

c) Write a function, autoComp which combines autoBass and autoChord. Given suitable definitions of twinkleMelody and twinkleChords different variations of  Twinkle Twinkle Little Star could then be generated by definitions like these:

    twinkleBasic   = twinkleMelody :=: autoComp basic (C, Major) twinkleChords
    twinkleCalypso = twinkleMelody :=: autoComp calypso (C, Major) twinkleChords
    twinkleBoogie  = twinkleMelody :=: autoComp boogie (C, Major) twinkleChords

And the calypso version for example might sound something like this.

d) Find the score of at least one other song of your own choice and use as a second test case. Since the assignment only gives tables for major keys you should of course choose a song in a major key. If you have problems finding a score, we have a small collection of songs you may use.

Note: You should be aware that different bass styles require different tempo to give a good sound and that the relative volume of the different voices (melody, chords, bass) can be rather important. You may have to do some experiments. While developing the functions you are recommended to ignore instrumentation (piano is default). But once the program is working you may want to try different instruments for the different voices, for example electric or acoustic bass for the bass voice and flute for the chord voicing.

Submission requirements

You are expected to submit three files for this assignment:

• autoComp.lhs which is literate Haskell module with the accompaniment generator. You are reminded that this file will be judged not only as a program but also as a written report.
• twinkle.hs which contains the melody and chord progression of Twinkle Twinkle Little Star and the corresponding application of the autoComp function
• <yourSong>.hs which is the melody and chord progression of the song you have used as your second test case.

These files together with an estimate of the number of hours spent on this assignment should no later than December 1st, 2014 be mailed to fp@cs.lth.se with the following subject line

Assignment 2 by username1 and username2

(where username1 and username2 are your logins).